Square of summation, difference of squares, cube of summation, summation of two cubes...
Advertisement:
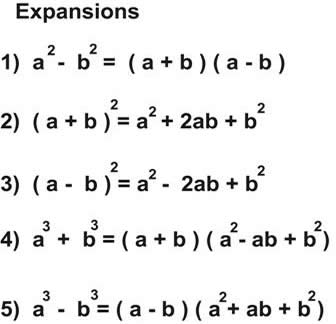
Read Later
Square of summation, difference of squares, cube of summation, summation of two cubes...
Related Links :
Expansions"Exponentiation is used extensively in many fields, including economics, biology, chemistry, physics, and computer science, with applications such as compound interest, population growth, chemical reaction kinetics, wave behavior, and public-key cryptography."
, Symbol for Number;
, Symbol for Number;
Algebra, branch of mathematics in which arithmetical operations and formal manipulations are applied to abstract symbols rather than specific numbers. The notion that there exists such a distinct subdiscipline of mathematics, as well as the term algebra to denote it, resulted from a slow historical development. This article presents that history, tracing the evolution over time of the concept of the equation, number systems, symbols for conveying and manipulating mathematical statements, and the modern abstract structural view of algebra. For information on specific branches of algebra, see elementary algebra, linear algebra, and modern algebra. Modern algebra, also called abstract algebra, branch of mathematics concerned with the general algebraic structure of various sets (such as real numbers, complex numbers, matrices, and vector spaces), rather than rules and procedures for manipulating their individual elements. During the second half of the 19th century, various important mathematical advances led to the study of sets in which any two elements can be added or multiplied together to give a third element of the same set. The elements of the sets concerned could be numbers, functions, or some other objects. As the techniques involved were similar, it seemed reasonable to consider the sets, rather than their elements, to be the objects of primary concern. A definitive treatise, Modern Algebra, was written in 1930 by the Dutch mathematician Bartel van der Waerden, and the subject has had a deep effect on almost every branch of mathematics.
Figure - 12.1 http://www.algebra4children.com/worked_examples/basic_expansions.jpg