Read Later

Introduction

Capacitance Formulas Calculator is programmed for helping you to use the formulas with respect to capacitance.

Description

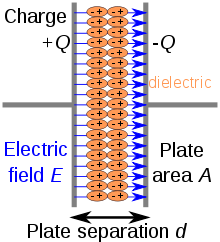
The combination of the electric field generated by the first plate and the electric field generated by the second plate is the electric field between two different plates charged. If the area of the plates and the distance between the plates are not changing(a constant), the combined charge and the voltage is proportional, this term called capacitance in physics.

$C$ , Symbol for Capacitance(in Farad);
$Q$ , Symbol for Charge(in Coulomb);
$V$ , Symbol for Voltage(in Volts);
$\in_{0}$ , Symbol for Vacuum Permittivity(Electric Constant);
$\in_{r}$ , Symbol for Relative Permittivity(Dielectric Constant);
$A$ , Symbol for Area(in Square Meters);
$d$ , Symbol for Separation(in Meters);
$W$ , Symbol for Work or Energy Stored(in Joules);
$σ$ , Symbol for Surface Charge Density(in farad / (square meter));
$C_{e q}$ , Symbol for Total Capacitance(in Farad);

Figure - 3.1

Quote from Britannica

Capacitance, property of an electric conductor, or set of conductors, that is measured by the amount of separated electric charge that can be stored on it per unit change in electrical potential. Capacitance also implies an associated storage of electrical energy. If electric charge is transferred between two initially uncharged conductors, both become equally charged, one positively, the other negatively, and a potential difference is established between them. The capacitance C is the ratio of the amount of charge q on either conductor to the potential difference V between the conductors, or simply C = q/V. In both the practical and the metre–kilogram–second scientific systems, the unit of electric charge is the coulomb and the unit of potential difference is the volt, so that the unit of capacitance—named the farad (symbolized F)—is one coulomb per volt. One farad is an extremely large capacitance. Convenient subdivisions in common use are one-millionth of a farad, called a microfarad (μF), and one-millionth of a microfarad, called a picofarad (pF; older term, micromicrofarad, μμF). In the electrostatic system of units, capacitance has dimensions of distance.

Formula 1:

C = \frac{Q}{V}

Output

Formula 2:

C = ε_{0} \times ε_{r} \times \frac{A}{d}

Output

Formula 3:

W = \frac{1}{2} C V^{2}

Output

Formula 4:

σ = Q / A

Output

Formula 5(in parallel):

- Enter $C_{n}$ values up to 'n' by using comma instead of space.

* If,

* $C_{1}$ = 2

* $C_{2}$ = 1.83

* $C_{3}$ = 3.05

* Enter 'n' = 3;

* Cn = 2,1.83,3.05

C_{e q} = {\sum C_{i}}_{i = 1}^{n} = C_{1} + C_{2} + C_{3} + \dots + C_{n}

Output

Formula 6(in serial):

- Enter $C_{n}$ values up to 'n' by using comma instead of space.

* If,

* $C_{1}$ = 2

* $C_{2}$ = 1.83

* $C_{3}$ = 3.05

* Enter 'n' = 3;

* Cn = 2,1.83,3.05

\frac{1}{C_{e q}} = {\sum \frac{1}{C_{i}}}_{i = 1}^{n} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} + \dots + \frac{1}{C_{n}}

Introduction

Tags

Share

Capacitance Formulas Calculator

Introduction

Tags

Share

Description

Quote from Britannica

Formula 1:

Output

Formula 2:

Output

Formula 3:

Output

Formula 4:

Output

Formula 5(in parallel):

Output

Formula 6(in serial):

Output