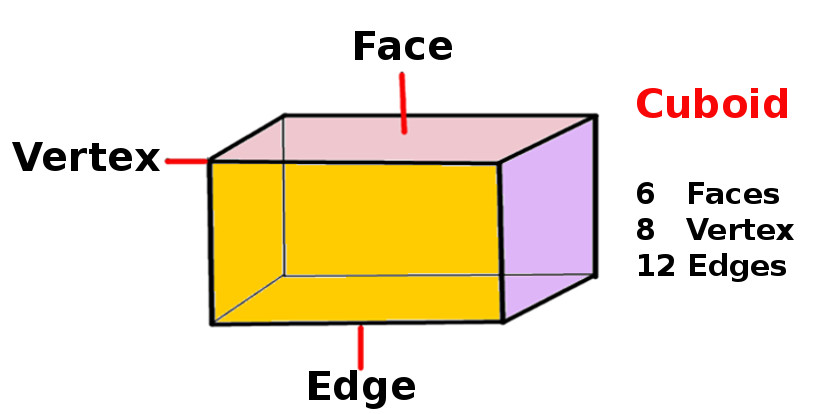
In geometry, a cuboid is a 3D shape which has three different sides and face diagonals. Calculate its volume, surface area and space diagonal.
Advertisement:
Read Later
In geometry, a cuboid is a 3D shape which has three different sides and face diagonals. Calculate its volume, surface area and space diagonal.
Related Links :
Cuboid FormulasIn geometry, a cuboid is a 3D shape which has three different sides and face diagonals. Calculate its volume, surface area and space diagonal.
, Symbol for Side;
, Symbol for Volume;
, Symbol for Surface area;
, Symbol for Space diagonal;
In geometry, a cuboid is a convex polyhedron bounded by six quadrilateral faces, whose polyhedral graph is the same as that of a cube. While mathematical literature refers to any such polyhedron as a cuboid,[1] other sources use "cuboid" to refer to a shape of this type in which each of the faces is a rectangle (and so each pair of adjacent faces meets in a right angle); this more restrictive type of cuboid is also known as a rectangular cuboid, right cuboid, rectangular box, rectangular hexahedron, right rectangular prism, or rectangular parallelepiped.[2] In a rectangular cuboid, all angles are right angles, and opposite faces of a cuboid are equal. By definition this makes it a right rectangular prism, and the terms rectangular parallelepiped or orthogonal parallelepiped are also used to designate this polyhedron. The terms "rectangular prism" and "oblong prism", however, are ambiguous, since they do not specify all angles. The square cuboid, square box, or right square prism (also ambiguously called square prism) is a special case of the cuboid in which at least two faces are squares. It has Schläfli symbol {4} × { }, and its symmetry is doubled from [2,2] to [4,2], order 16. The cube is a special case of the square cuboid in which all six faces are squares. It has Schläfli symbol {4,3}, and its symmetry is raised from [2,2], to [4,3], order 48.
Figure - 18.1 http://images.algebraden.com/geometry/big/cuboid.jpg