By using this web-tool, calculate the volume, lateral surface and radius of a cylinder easily.
Advertisement:
Read Later
By using this web-tool, calculate the volume, lateral surface and radius of a cylinder easily.
Related Links :
Cylinder FormulasBy using this web-tool, calculate the volume, lateral surface and radius of a cylinder easily.
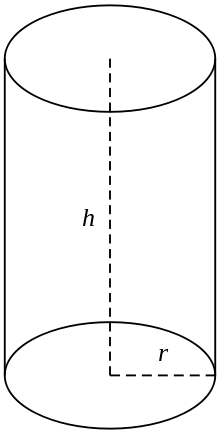
, Symbol for Radius;
, Symbol for Height;
, Symbol for Volume;
, Symbol for Lateral surface;
Cylinder, in geometry, surface of revolution that is traced by a straight line (the generatrix) that always moves parallel to itself or some fixed line or direction (the axis). The path, to be definite, is directed along a curve (the directrix), along which the line always glides. In a right circular cylinder, the directrix is a circle. The axis of this cylinder is a line through the centre of the circle, the line being perpendicular to the plane of the circle. In an oblique circular cylinder, the angle that the axis makes with the circle is other than 90°. The directrix of a cylinder need not be a circle, and if the cylinder is right, planes parallel to the plane of the directrix that intersect the cylinder produce intersections that take the shape of the directrix. For such a plane, if the directrix is an ellipse, the intersection is an ellipse. The generatrix of a cylinder is assumed to be infinite in length; the cylinder so generated, therefore, extends infinitely in both directions of its axis. A finite cylinder has a finite base, the surface enclosed by the directrix, and a finite length of generatrix, called an element.
Figure - 29.1 By User:Ævar Arnfjörð Bjarmason - Image:Cylinder (geometry).png, Public Domain, https://commons.wikimedia.org/w/index.php?curid=776995