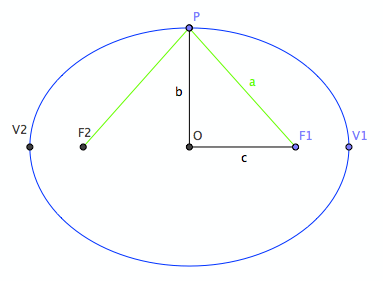
An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r_1 and r_2 from two fixed points F_1 and F_2 (the foci) separated by a distance of 2c is a given positive constant 2a (Hilbert and Cohn-Vossen 1999, p. 2).
Advertisement:
Read Later
An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r_1 and r_2 from two fixed points F_1 and F_2 (the foci) separated by a distance of 2c is a given positive constant 2a (Hilbert and Cohn-Vossen 1999, p. 2).
Related Links :
Ellipse FormulasAn ellipse is a curve that is the locus of all points in the plane the sum of whose distances r_1 and r_2 from two fixed points F_1 and F_2 (the foci) separated by a distance of 2c is a given positive constant 2a (Hilbert and Cohn-Vossen 1999, p. 2).
, Symbol for Area;
, The length of semi-major axis;
, The length of semi-minor axis;
Ellipse, a closed curve, the intersection of a right circular cone (see cone) and a plane that is not parallel to the base, the axis, or an element of the cone. It may be defined as the path of a point moving in a plane so that the ratio of its distances from a fixed point (the focus) and a fixed straight line (the directrix) is a constant less than one. Any such path has this same property with respect to a second fixed point and a second fixed line, and ellipses often are regarded as having two foci and two directrixes. The ratio of distances, called the eccentricity, is the discriminant (q.v.; of a general equation that represents all the conic sections [see conic section]). Another definition of an ellipse is that it is the locus of points for which the sum of their distances from two fixed points (the foci) is constant. The smaller the distance between the foci, the smaller is the eccentricity and the more closely the ellipse resembles a circle. A straight line drawn through the foci and extended to the curve in either direction is the major diameter (or major axis) of the ellipse. Perpendicular to the major axis through the centre, at the point on the major axis equidistant from the foci, is the minor axis. A line drawn through either focus parallel to the minor axis is a latus rectum (literally, “straight side”). The ellipse is symmetrical about both its axes. The curve when rotated about either axis forms the surface called the ellipsoid (q.v.) of revolution, or a spheroid.
Figure - 25.1 http://xahlee.info/SpecialPlaneCurves_dir/Ellipse_dir/ellipse.png