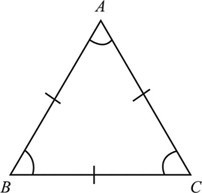
An equilateral triangle is a triangle with all three sides of equal length a, corresponding to what could also be known as a "regular" triangle.
Advertisement:
Read Later
An equilateral triangle is a triangle with all three sides of equal length a, corresponding to what could also be known as a "regular" triangle.
Related Links :
Equilateral Triangle FormulasAn equilateral triangle is a triangle with all three sides of equal length a, corresponding to what could also be known as a "regular" triangle.
, Symbol for Area;
, Symbol for Side;
, Symbol for Height;
In geometry, an equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle. Morley's trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle. Napoleon's theorem states that, if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, the centers of those equilateral triangles themselves form an equilateral triangle. A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.[12]
Figure - 26.1 https://cramster-image.s3.amazonaws.com/definitions/DC-2414V2.png