A hexagon is a six-sided polygon, which means that it has six equal side. Calculate its diagonal, short diagonal, perimeter and area.
Advertisement:
Read Later
A hexagon is a six-sided polygon, which means that it has six equal side. Calculate its diagonal, short diagonal, perimeter and area.
Related Links
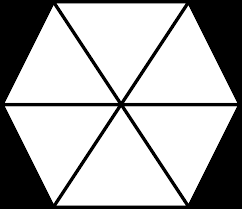
Hexagon FormulasA hexagon is a six-sided polygon, which means that it has six equal side. Calculate its diagonal, short diagonal, perimeter and area.
, Symbol for Side(edge);
, Symbol for Diagonal;
, Symbol for Short diagonal;
, Symbol for Perimeter;
, Symbol for Area;
A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle, which equals {\displaystyle {\tfrac {2}{\sqrt {3}}}} {\displaystyle {\tfrac {2}{\sqrt {3}}}} times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has 6 rotational symmetries (rotational symmetry of order six) and 6 reflection symmetries (six lines of symmetry), making up the dihedral group D6. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles. Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.
Figure - 15.1 https://www.varsitytutors.com/intermediate_geometry-help/how-to-find-the-length-of-the-diagonal-of-a-hexagon