In geometry, a kite is described as a quadrilateral having 2 pairs of equal sides which are adjacent to each other.
Advertisement:
Read Later
In geometry, a kite is described as a quadrilateral having 2 pairs of equal sides which are adjacent to each other.
Related Links
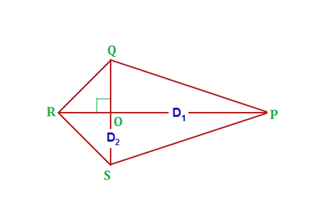
Kite FormulasIn geometry, a kite is described as a quadrilateral having 2 pairs of equal sides which are adjacent to each other.
, Symbol for Area;
, Symbol for Short diagonal;
, Symbol for Long diagonal;
In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other rather than adjacent. Kite quadrilaterals are named for the wind-blown, flying kites, which often have this shape and which are in turn named for a bird. Kites are also known as deltoids, but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object. A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle. If all four sides of a kite have the same length (that is, if the kite is equilateral), it must be a rhombus. If a kite is equiangular, meaning that all four of its angles are equal, then it must also be equilateral and thus a square. A kite with three equal 108° angles and one 36° angle forms the convex hull of the lute of Pythagoras.[1] The kites that are also cyclic quadrilaterals (i.e. the kites that can be inscribed in a circle) are exactly the ones formed from two congruent right triangles. That is, for these kites the two equal angles on opposite sides of the symmetry axis are each 90 degrees.[2] These shapes are called right kites[3] and they are in fact bicentric quadrilaterals (below to the left). Among all the bicentric quadrilaterals with a given two circle radii, the one with maximum area is a right kite.[4]
Figure - 21.1 https://byjus.com/area-of-a-kite-formula