Read Later

Introduction

Projectile motion formulas indicate how an object(a projectile) moves and behaves under the action of gravity by defining the trajectory of the object, which is also called the ballistic trajectory.

Description

Projectile motion formulas indicate how an object(a projectile) moves and behaves under the action of gravity by defining the trajectory of the object, which is also called the ballistic trajectory.

$v$ , Symbol for Velocity(in Meter per seconds);
$t$ , Symbol for Time(in Seconds);
$x$ , Symbol for Horizontal Displacement(in Meters);
$y$ , Symbol for Vertical Displacement(in Meters);
$g$ , Symbol for The acceleration of gravity(in Meter per second square);
$a$ , Symbol for Acceleration(in Meter per second square);
$d$ , Symbol for Displacement(in Meters);

Figure - 10.1

Quote from Britannica

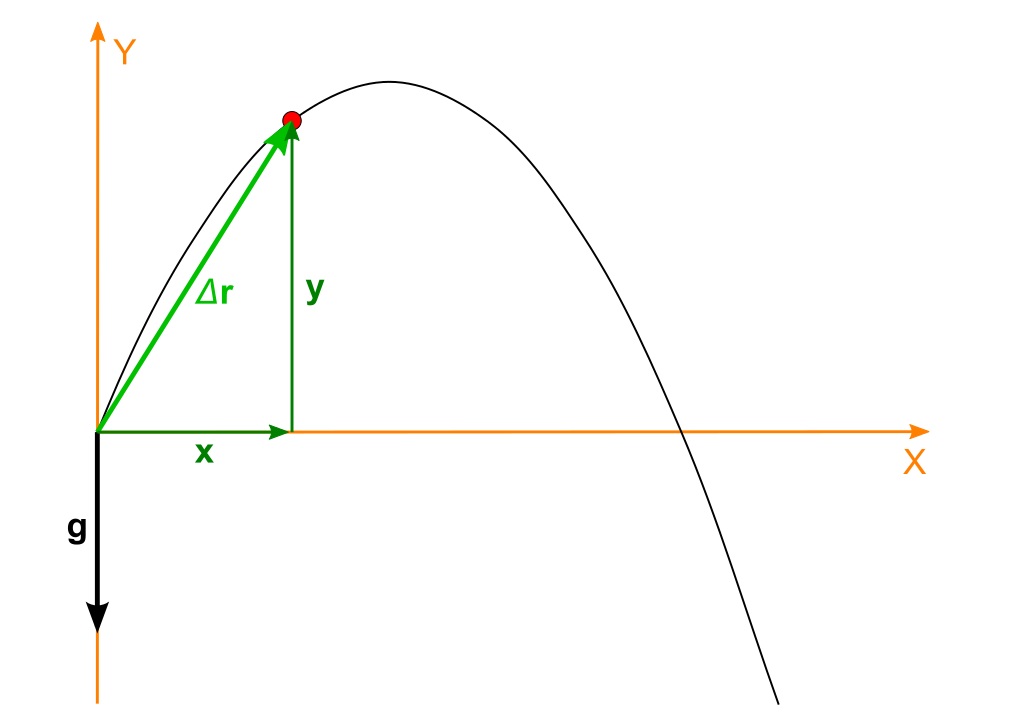
Galileo was quoted above pointing out with some detectable pride that none before him had realized that the curved path followed by a missile or projectile is a parabola. He had arrived at his conclusion by realizing that a body undergoing ballistic motion executes, quite independently, the motion of a freely falling body in the vertical direction and inertial motion in the horizontal direction. These considerations, and terms such as ballistic and projectile, apply to a body that, once launched, is acted upon by no force other than Earth’s gravity.

Horizontal Displacement

x = v_{x} t

Output

Vertical Displacement

y = v_{y} t - \frac{1}{2} g t^{2}

Output

Final Velocity

(v_{2})^{2} = (v_{1})^{2} + 2 a d

Output

The magnitude of the velocity

v = \sqrt{{v_{x}}^{2} + {v_{y}}^{2}}

Output

References

^{Figure - 10.1} By Zátonyi Sándor, (ifj.) Fizped - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18893493

Introduction

Tags

Share

Projectile Motion Calculator

Introduction

Tags

Share

Description

Quote from Britannica

Horizontal Displacement

Output

Vertical Displacement

Output

Final Velocity

Output

The magnitude of the velocity

Output

References