In geometry, a trapezoid is described as a quadrilateral having at least one pair of parallel sides.
Advertisement:
Read Later
In geometry, a trapezoid is described as a quadrilateral having at least one pair of parallel sides.
Related Links :
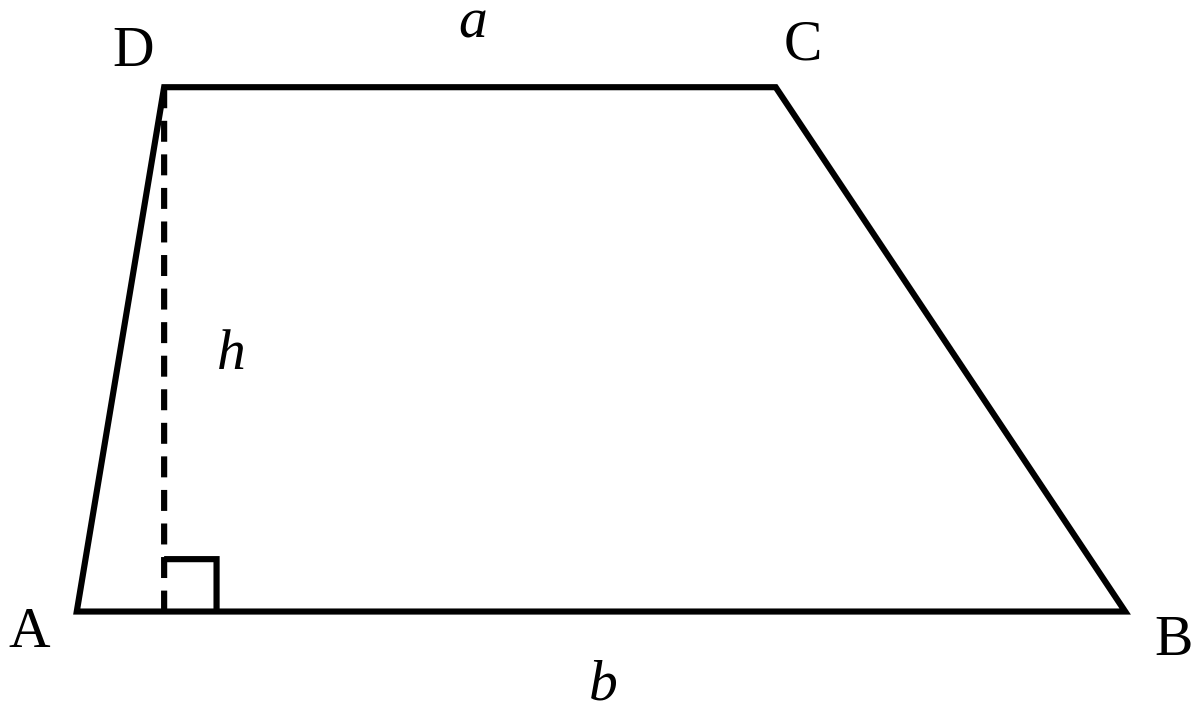
Trapezoid FormulasIn geometry, a trapezoid is described as a quadrilateral having at least one pair of parallel sides.
, Symbol for Area;
, Symbol for Base;
, Symbol for Height;
In Euclidean geometry, a convex quadrilateral with at least one pair of parallel sides is referred to as a trapezoid[1][2] (/ˈtræpəzɔɪd/) in American and Canadian English but as a trapezium (/trəˈpiːziəm/) in English outside North America. The parallel sides are called the bases of the trapezoid and the other two sides are called the legs or the lateral sides (if they are not parallel; otherwise there are two pairs of bases). A scalene trapezoid is a trapezoid with no sides of equal measure. The term trapezium has been in use in English since 1570, from Late Latin trapezium, from Greek τραπέζιον (trapézion), literally "a little table", a diminutive of τράπεζα (trápeza), "a table", itself from τετράς (tetrás), "four" + πέζα (péza), "a foot; end, border, edge".[4] The first recorded use of the Greek word translated trapezoid (τραπεζοειδή, trapezoeidé, "table-like") was by Marinus Proclus (412 to 485 AD) in his Commentary on the first book of Euclid's Elements.[5] This article uses the term trapezoid in the sense that is current in the United States and Canada. In many other languages using a word derived from the Greek for this figure, the form closest to trapezium (e.g. Portuguese trapézio, French trapèze, Italian trapezio, Spanish trapecio, German Trapez, Russian "трапеция") is used.
Figure - 22.1 By No machine-readable author provided. WikedKentaur assumed (based on copyright claims). - No machine-readable source provided. Own work assumed (based on copyright claims)., Public Domain, https://commons.wikimedia.org/w/index.php?curid=708515